Adaptive Importance Sampling: The Past, the Present, and the Future

Contributed by Dr. Victor Elvira and based on the article published in the IEEE Signal Processing Magazine, July 2017, available in IEEE Xplore®.

Dr. Elvira also presented this topic in a 2019 SPS Education webinar. Visit the recorded webinar at the SPS Resource Center.

Monte Carlo (MC) methods are a set of fascinating computational techniques that have attracted ever-increasing attention in the last decades. They are based on the simulation of random samples that are used for diverse purposes, such as numerical integration or optimization. MC was first applied systematically by the Italian physicist Enrico Fermi when he studied neutron diffusion, however, he never published any paper on this topic. Later, the methodology came to be known as MC sampling. The MC methods, in the way we know them today, were created by Stanislaw Ulam, John von Neumann, and others, mostly at Los Alamos National Laboratory (USA). Their efforts coincided with the development of the first general computer, the ENIAC, and resulted in the Metropolis algorithm, named after the physicist Nicholas Metropolis. The reader is invited to deepen into the history of the Monte Carlo methodology through the scientific popularization article [Metropolis, 1987] written by Nicholas Metropolis himself. The next major advancement of MC methods came with a generalization of the Metropolis algorithm proposed by Hastings in 1970, yielding the widely known Metropolis-Hastings algorithm.

Importance Sampling (IS) is a different family of MC methods whose basic idea started to be developed also in the early fifties of last century. Unlike the case of the Metropolis algorithm, it is difficult to track back a precise origin of the IS methodology. It was implicitly present in statistical physics for inference of rare events, and in particular for estimating the probability of nuclear particles that penetrate shields [Kahn, 1950]. Later, IS was also used as a variance reduction technique based on simulating from a proposal density instead of the target density. The interest in IS techniques was running in parallel to the emergence of Bayesian computational methods. The interest was not only driven by their simplicity, but also by their ability to estimate normalizing constants of the target distribution, a feature not shared by MCMC methods that turns out useful in many practical problems (e.g., model selection).

Due to several factors, including the rise of the Bayesian estimation approach in the last decade, the interest in MC methods in the signal processing community has greatly increased. In particular, within the Bayesian signal processing framework, these problems are addressed by constructing posterior probability distributions of the unknowns. The posteriors combine all the information about the unknowns in the observations with the information that is present in their prior probability distributions. Given the posterior, one often wants to make inference about the unknowns, e.g., if we are estimating parameters, finding the values that maximize their posterior, or the values that minimize some cost function given the uncertainty of the parameters. Unfortunately, obtaining closed-form solutions to these types of problems is infeasible in most practical applications, and therefore, developing approximate inference techniques is of utmost interest. The IS methodology comes to the rescue for solving most difficult problems of inference is based on random drawing of samples.

The IS methods are elegant, theoretically sound, simple-to-understand, and widely applicable. IS also allows for the approximation of complicated distributions, especially in the case where sampling from those distributions is not possible. Assume that the aim is to approximate a given target probability distribution. In its plain version, IS uses a so-called proposal distribution to simulate random samples, that are then weighted in order to produce consistent estimators of intractable integrals. Then, the basic IS mechanism consists of (a) drawing samples from so-called proposal densities, (b) weighting the samples by accounting for the mismatch between the target and the proposal densities, and (c) performing the desired inference using the weighted samples.

However, the efficiency of IS relies on the choice of an appropriate proposal distribution to produce relevant samples for the integral we are trying to approximate.  It is well known that the performance of IS methods directly depends on the choice of the proposal densities [Robert, 2004]. When the method is applied naively, only few of the IS weights take relevant values, while the rest are negligible. This undesired phenomenon is widely known in the IS literature as weight degeneracy [Robert, 2004]. For example, if the goal is to estimate the mean of the target distribution, then the proposals must be adapted to parts of the space where the posterior probability is large, while if the focus is on a problem related to system reliability, then the probability of rare events is better approximated by placing the proposals in the tails of the posterior. Locating the regions from which samples should be drawn may not be easy, which suggests that the main challenge in implementing IS methods lies in finding good proposal densities. However, designing these proposals usually cannot be done a priori, and thus, adaptive procedures must be constructed and applied iteratively. The objective is that with passing iterations, the quality of the samples improves and the inference from them becomes more accurate. This leads us to the concept of adaptive importance sampling (AIS). AIS methods are endowed with the nice feature of being able to learn from previously sampled values of the unknowns and consequently, to become more accurate. It is important to note that the AIS algorithms must remain simple, i.e., both the drawing of samples and the computation of their weights should be easily managed.

In this feature article, we first go over the basics of IS and then proceed with explaining the learning process that takes place in AIS and with presenting several state-of-the-art methods. We discuss AIS estimators and their convergence properties, and then show numerical results on signal processing examples. Our aim is widening the use of AIS and contribute to disseminate the interest in researching novel AIS methods that will overcome the current limitations of the methodology.

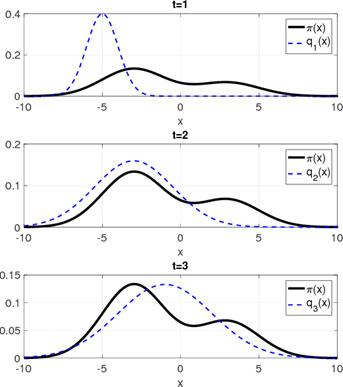
Proposal adaptation through AIS. The initial proposal q1(x) (too narrow and poorly placed) is iteratively moved towards a better location at some intermediate location between the two modes of the target pdf and widened in order to properly cover the effective support of the target.

(Figure and caption from M. F. Bugallo, V. Elvira, L. Martino, D. Luengo, J. Miguez and P. M. Djuric, "Adaptive Importance Sampling: The past, the present, and the future," in IEEE Signal Processing Magazine, vol. 34, no. 4, pp. 60-79, July 2017,
doi: 10.1109/MSP.2017.2699226.)

References:

N. Metropolis, “The beginning of the Monte Carlo method,” Los Alamos Sci., no. 15, pp. 125-130, 1987.

H. Kahn, “Random sampling (Monte Carlo) techniques in neutron attenuation problems,” Nucleonics, vol. 6, no. 5, pp. 27-33, 1950.

C. P. Robert and G. Casella, Monte Carlo Statistical Methods. New York: Springer-Verlag, 2004.