Contributed by Dr. Aykut Koç, based on the IEEEXplore® article, “Multivariate Time Series Imputation With Transformers” published in the IEEE Signal Processing Letters on 25 November 2022, and the SPS Webinar, “Devising Transformers as an Autoencoder for Unsupervised Multivariate Time Series Imputation”, available on the SPS Resource Center.
Introduction
The processing of time-series data is ubiquitous in various application areas, encompassing health care [1], transportation [2], and weather forecasting [3]. Specifically, multivariate time-series data manifest a correlated sequence over a shared independent variable, exemplified by simultaneous sensor recordings in tasks like autonomous driving maneuvers or diverse channels within data ac quisition devices employed in clinical diagnoses. At the same time, the increasing frequency of data acquisition failures, such as sensor malfunctions or human errors, has become more common, which results in missing values in the data and loss of significant amount of information. To solve these challenging issues, several imputation methods have been developed to fill the missing patterns in data.
Earlier imputation methods rely on shallow models, making significant assumptions about missing patterns. These assumptions involve techniques such as interpolation, mean averaging, and k-nearest neighbors. Recently, there has been a shift towards deep learning-based methods, including state-of-the-art models such as recurrent neural networks (RNNs), generative-adversarial networks (GANs), and diffusion models, which have offered sophisticated solutions and demon strated notable performance improvements. Moreover, transformer architectures have become increasingly popular due to their incorporation of self-attention mechanism, which highlights im portant input features without relying on sequence-aligned convolutions or recurrent models. This allows for successful adaptations to long-term dependencies in time-series data [4].
Inspired by the capabilities of transformer models, we introduce a novel method named Multi variate Time-Series Imputation with Transformers (MTSIT). This entails an unsupervised autoen coder model featuring a transformer encoder, leveraging unlabeled observed data for simultaneous reconstruction and imputation of multivariate time-series. The training of our autoencoder involves stochastically masking and imputing non-missing values, utilizing a training objective specifically crafted for multivariate time-series data [4].
The Proposed Method
In this work, we establish an unsupervised approach for imputation task where an autoencoder is trained by stochastically-masking the non-missing (observed) values and teaching the network to impute them. At the test stage, the trained autoencoder show proficiency in imputing both actual missing values and those artificially generated for training purposes. Fig. 1 illustrates our stochas tic masking setup, autoencoder architecture and MTSIT training strategy. The MTSIT strategy involves presenting an input sequence with gaps (represented by gray shadows) to the transformer encoder. The final encoder block produces an output sequence that is linearly transformed into the imputed sequence. The Mean Squared Error (MSE) is subsequently computed between the missing values and their predicted imputations, guiding the network’s training towards minimizing the MSE.
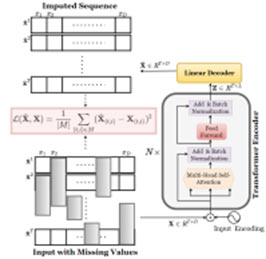
Figure 1: Overview of the proposed method.
Experiments and Results
To demonstrate the effectiveness of our approach, we evaluated our method on two benchmark datasets Healthcare from the PhysioNet Challenge 2012 [5] and the Beijing Air Quality [6]. In performance comparison, our method consistently outperforms seven state-of-the-art imputation methods significantly almost in all training schemes. We also illustrate our method’s imputation performance in Fig. 2 for both datasets.
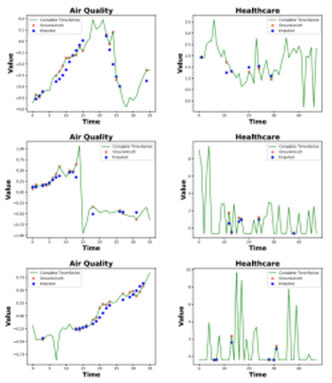
Figure 2: Imputation examples on both datasets
References:
[1] Z. Hajihashemi and M. Popescu, "A Multidimensional Time-Series Similarity Measure With Applications to Eldercare Monitoring," in IEEE Journal of Biomedical and Health Informatics, vol. 20, no. 3, pp. 953-962, May 2016, doi: https://dx.doi.org/10.1109/JBHI.2015.2424711.
[2] A. Gupta, H. P. Gupta, B. Biswas and T. Dutta, "An Early Classification Approach for Multivariate Time Series of On-Vehicle Sensors in Transportation," in IEEE Transactions on Intelligent Transportation Systems, vol. 21, no. 12, pp. 5316-5327, Dec. 2020, doi: https://dx.doi.org/10.1109/TITS.2019.2957325.
[3] Y. Zheng, X. Yi, M. Li, R. Li, Z. Shan, E. Chang, and T. Li, “Forecasting fine-grained air quality based on big data,” in Proceedings of the 21th ACM SIGKDD international conference on knowledge discovery and data mining, pp. 2267–2276, 2015, https://doi.org/10.1145/2783258.2788573.
[4] A. Y. Yıldız, E. Ko¸c, and A. Ko¸c, “Multivariate time series imputation with transformers,” IEEE Signal Processing Letters, vol. 29, pp. 2517–2521, 2022, https://dx.doi.org/10.1109/LSP.2022.3224880.
[5] I. Silva, G. Moody, D. J. Scott, L. A. Celi, and R. G. Mark, “Predicting in-hospital mortality of icu patients: The physionet/computing in cardiology challenge 2012,” in 2012 Computing in Cardiology, pp. 245–248, IEEE, 2012.
[6] S. Zhang, B. Guo, A. Dong, J. He, Z. Xu, and S. X. Chen, “Cautionary tales on air-quality improvement in beijing,” Proceedings of the Royal Society A: Mathematical, Physical and En gineering Sciences, vol. 473, no. 2205, p. 20170457, 2017.
