
Contributed by Ahmet M. Elbir, Kumar Vijay Mishra, Sergiy A. Vorobyov and Robert W. Heath, Jr., based on the IEEEXplore® article, “Twenty-Five Years of Advances in Beamforming: From convex and nonconvex optimization to learning techniques,” published in the 75th Anniversary Edition of the IEEE Signal Processing Magazine in June 2023, and the 75th Anniversary Webinar with the same title, available on the SPS Resource Center.
Introduction
Beamforming is a widely used signal processing technique that exploits arrays of sensors improve one of many possible application-driven performance objectives [1]. It finds applications in several engineering applications such as radar, sonar, wireless communications, acoustics, astronomy, seismology, and medical imaging. Recent advances in mobile communications, usage of large arrays, high-frequency sensors, near-field signal recovery, and smart radio environments have opened interesting and novel signal processing problems in beamforming (Fig. 1). This post summarizes the evolution of beamforming algorithms as encapsulated in our recent article “Twenty-Five Years of Advances in Beamforming: From convex and nonconvex optimization to learning techniques” published in the IEEE Signal Processing Magazine.
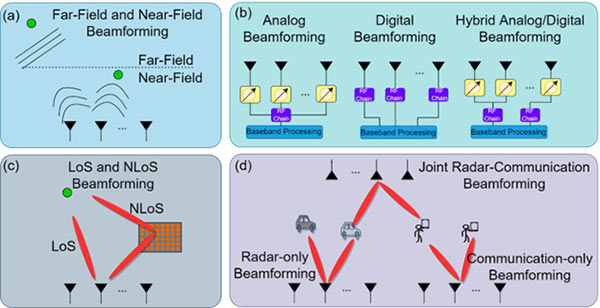
Figure 1. Major classes of beamforming techniques by (a) transmission range: far and near fields; (b) transceiver architectures: analog, digital, and hybrid beamforming; (c) paths: line-of-sight (LoS) and and non-LoS (NLoS) beamforming, wherein the NLoS path is controlled via joint active (transmitter) and passive (intelligent reflecting surface) devices; (d) applications: radar, communications, and joint radar-communications.
Early Beamforming Days
Italian electrical engineer Guglielmo Marconi is credited for the first scientific experiments with beamforming. He used a circular array with four antennas to improve the gain of trans-Atlantic Morse code transmission in 1901. A similar early demonstration of gains provided by a phased array to direct radio waves was in 1905 by Karl Ferdinand Braun, who shared Nobel Prize in physics with Marconi in 1909 for their contributions to wireless telegraphy. In the 1940s, antenna diversity as a technique to overcome fading was developed for phased array radars and radio astronomy. During the 1950-1960s, with the development of phased arrays for sonars, the steering of signals with antenna arrays was no longer restricted to electromagnetic waves.
Adaptive beamforming, wherein a processor at the antenna back-end updates and compensates the array weights [2], emerged in the 1960s. This opened the door to the subsequent development of different algorithms for updating the weights and the introduction of numerous criteria for establishing the optimality of the weights. One of the first formal approaches was proposed by J. Capon, who proposed selecting the weight vectors or beamformers to minimize the array output power. The Capon beamformer is subjected to the linear constraint that the signal-of-interest does not suffer from any distortion, e.g., direction mismatch, signal fading, and local scattering. Hence, this technique is also usually referred to as the minimum variance (MV) distortionless response (MVDR) beamforming.
From here, we delineate the evolution of mathematical frameworks for beamforming starting in the mid-1990s. We classify their evolution based on the mathematical principles used in the optimum selection of weights: convex, nonconvex, and learning-based approaches.
Late 1990s-Early 2000s: Convex Beamforming
In the late 1990s and early 2000s, significant progress was made toward robust beamformer design by exploiting convex optimization [5], which recast originally difficult-to-design beamformers as computationally attractive problems that yield exact or approximate solutions through algorithms, such as interior-point methods. These methods typi2cally consider minimizing the effect of mismatches in the array steering vectors and the look direction based on the worst-case performance optimization [3].
The applications of convex beamformers have traditionally advanced from the simple exact Capon approach to more complex transmit, multicast, network, and distributed beamformers. In general, their goal is to improve the robustness against errors/mismatches in the look direction, array manifold, and local scattering. These techniques were limited to only the specific mismatch they treat [3], thereby giving rise to early generalization of robust beamforming approaches such as sample matrix inversion algorithm, robust Capon beamforming, eigenspace-based beamformer, worst-case performance optimization, and general-rank beamformer [4].
Late 2000s: Non-convex Beamforming
During the late 2000s, certain applications of beamforming that have nonconvex objective functions or constraints gained salience. They tackle the design problem by recasting or relaxing it into tractable convex forms. This may be achieved by dropping the nonconvex constraints or decoupling the beamforming design into multiple convex subproblems. These included robust adaptive beamforming with additional constraints related to the positive semi-definiteness of the signal covariance matrix norm of the steering vectors, and stochastic distortionless response; multicast transmit beamforming and hybrid (analog/digital) beamforming [6].
In the last decade, with the advent of new cellular communications technologies, beamforming has been extensively investigated for multi-antenna systems [6]. The 5G systems (2019-present) offer support for larger antenna arrays as well as communication at millimeter wave (mmWave). To reduce the hardware, cost, power, and area in mmWave massive systems, hybrid (analog and digital) beamforming has been introduced [6]. Unlike a conventional digital beamformer employing a single radio-frequency (RF) chain dedicated to each antenna, hybrid approaches employ a few (large) RF chains (analog components, e.g., phase shifters) to reduce the hardware cost (Figure 2). The hybrid beamformer design is also nonconvex because of the product of analog and digital beamformers and the unit-modulus constraint owing to the use of phase shifters in the analog beamformers.
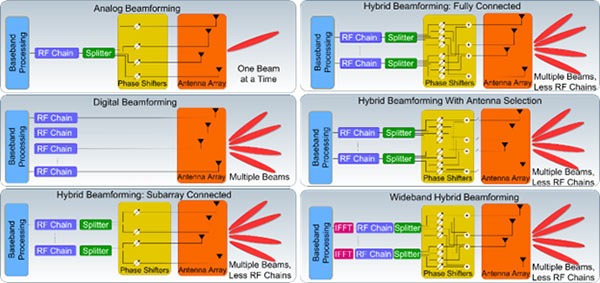
Figure 2. The transmitter architectures for (a) analog, (b) digital, and (c)–(f) hybrid beamforming. Analog beamforming generates only one beam because it employs a single RF chain. On the other hand, multiple beams are obtained via digital beamformers but at the cost of multiple RF chains. It is possible to generate multiple beams with fewer RF chains in the hybrid approach through configurations such as (c) subarray connected, (d) fully connected, (e) sparse antenna-selective, and (f) wideband architectures. IFFT: inverse fast Fourier transform.
Late 2010s-present: Learning-based Beamforming
Very recently, data-driven methods such as machine learning (ML) have been leveraged to obtain beamformers [7]. ML is a subset of artificial intelligence (AI) that allows neural networks (NNs) to learn directly from precedents, data, and examples without being explicitly programmed. Many beamformers involve nonlinear operations. In this context, NNs are particularly attractive because they successfully approximate non-linear functions or predict the class of a function that is divided by a non-linear decision boundary. In learning-based hybrid beamforming, the problem is approached from a model-free viewpoint by constructing a nonlinear mapping between the input data (e.g., the channel matrix and array output) and output (beamformers) of a learning model. Figure 3 shows various applications of ML in wireless communications.
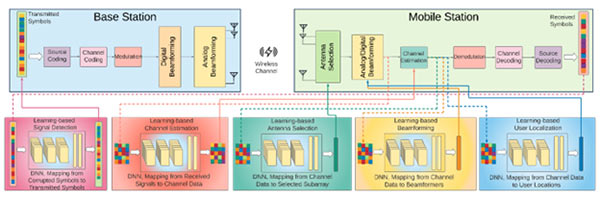
Figure 3. Various applications of ML for wireless communications on symbol detection, channel estimation, beamforming, antenna selection and localization.
Learning-based methods have the following advantages over model-based techniques:
- The model-free/data-driven structure of a learning-based approach yields a robust performance in terms of spectral efficiency against the corruptions (e.g., imperfectly estimated channel gain and path directions) in the input.
- Learning techniques extract feature patterns in the data. Hence, they easily update incoming/future data and adapt in response to environmental changes.
- Learning exhibits lower computational complexity in the prediction stage than optimization.
- Learning techniques can more easily work with other kinds of side information obtained for example from signals extracted at different operating frequencies [8].
Figure 4 compares the hybrid beamforming performance of learning-based [7] and model-based techniques, such as orthogonal matching pursuit (OMP) in [6] as well as the fully digital beamformer in terms of spectral efficiency. We observe that learning-based approach outperforms OMP. This is because the learning model is trained with the optimum beamformer weight as labels as compared to the suboptimum beamformers obtained by the OMP algorithm.
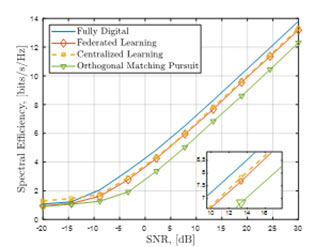
Figure 4. Hybrid beamforming performance of learning-based and model-based techniques.
Figure 5 summarizes the very interesting possibilities of different AI/ML algorithms in devising beamformers under different applications and constraints.
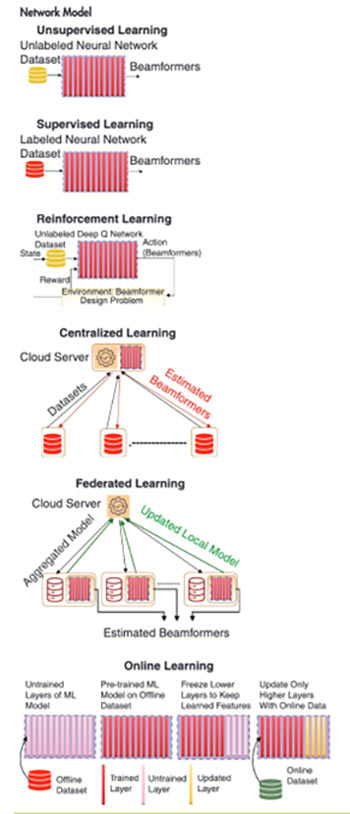
Figure 5. Learning models for designing beamformers. Unsupervised and supervised learning work with unlabeled and labeled datasets, respectively. Reinforcement learning operates on unlabeled data using a penalty-reward mechanism. Centralized (federated) learning trades-off overhead (accuracy) for performance (overhead). Online learning provides robustness against deviations of the prediction stage data from the training data.
Summary and Future Outlook
Research in beamforming continues to be highly active considering many emerging applications and theoretical advances. We captured the evolution of beamforming techniques in signal processing by covering two major technological leaps in the field, i.e., from convex to non-convex optimization and then to learning-based beamforming. We presented an overview of beamforming techniques that had a considerable impact on signal processing community for the challenging problems mainly focused on radar systems and wireless communications. The many beamforming algorithms, their possible variants, and their relative advantages provide a swiss-knife approach to choosing the most appropriate technique for a specific application.
References:
[1] B. D. Van Veen and K. M. Buckley, "Beamforming: A versatile approach to spatial filtering," in IEEE ASSP Magazine, vol. 5, no. 2, pp. 4-24, April 1988, doi: https://dx.doi.org/10.1109/53.665.
[2] J. Capon, "High-resolution frequency-wavenumber spectrum analysis," in Proceedings of the IEEE, vol. 57, no. 8, pp. 1408-1418, Aug. 1969, doi: https://dx.doi.org/10.1109/PROC.1969.7278.
[3] S. A. Vorobyov, A. B. Gershman and Zhi-Quan Luo, "Robust adaptive beamforming using worst-case performance optimization: a solution to the signal mismatch problem," in IEEE Transactions on Signal Processing, vol. 51, no. 2, pp. 313-324, Feb. 2003, doi: https://dx.doi.org/10.1109/TSP.2002.806865.
[4] A. M. Elbir, K. V. Mishra, S. A. Vorobyov and R. W. Heath, "Twenty-Five Years of Advances in Beamforming: From convex and nonconvex optimization to learning techniques," in IEEE Signal Processing Magazine, vol. 40, no. 4, pp. 118-131, June 2023, doi: https://dx.doi.org/10.1109/MSP.2023.3262366.
[5] A. B. Gershman, N. D. Sidiropoulos, S. Shahbazpanahi, M. Bengtsson and B. Ottersten, "Convex Optimization-Based Beamforming," in IEEE Signal Processing Magazine, vol. 27, no. 3, pp. 62-75, May 2010, doi: https://dx.doi.org/10.1109/MSP.2010.936015.
[6] O. E. Ayach, S. Rajagopal, S. Abu-Surra, Z. Pi and R. W. Heath, "Spatially Sparse Precoding in Millimeter Wave MIMO Systems," in IEEE Transactions on Wireless Communications, vol. 13, no. 3, pp. 1499-1513, March 2014, doi: https://dx.doi.org/10.1109/TWC.2014.011714.130846.
[7] A. M. Elbir, K. V. Mishra, M. R. B. Shankar and B. Ottersten, "A Family of Deep Learning Architectures for Channel Estimation and Hybrid Beamforming in Multi-Carrier mm-Wave Massive MIMO," in IEEE Transactions on Cognitive Communications and Networking, vol. 8, no. 2, pp. 642-656, June 2022, doi: https://dx.doi.org/10.1109/TCCN.2021.3132609.
[8] N. Gonzalez-Prelcic, A. Ali, V. Va and R. W. Heath, "Millimeter-Wave Communication with Out-of-Band Information," in IEEE Communications Magazine, vol. 55, no. 12, pp. 140-146, Dec. 2017, doi: https://dx.doi.org/10.1109/MCOM.2017.1700207.
