Empirical Wavelets

Contributed by Dr. Jérôme Gilles, based on the IEEEXplore® article, Empirical Wavelet Transform.

Adaptive, i.e., data-driven, methods have become very popular these last decades. If machine learning, and more specifically neural networks, are among the most used techniques these days, other approaches have been developed which, for instance, do not require  any  training.  The  Hilbert-Huang  trans- form, which combines the empirical mode decomposition (EMD) and the Hilbert transform, has proven to be efficient in extracting accurate time-frequency rep- resentation of non-stationary signals. The EMD step aims at decomposing the signal into its harmonic modes (i.e., amplitude modulated-frequency modulated constituents) such that their time-frequency information can be easily extracted. The main drawback of the EMD is its purely algorithmic aspect and lack of solid theoretical foundations which prevent to fully understand and predict its behav- ior. To overcome this issue, we propose the construction of adaptive wavelets [1], called empirical wavelets, to replace the EMD step.

Taking a wavelets point of view is motivated by two main reasons: 1) some experiments done on the EMD suggest that it behaves as an adaptive filter bank, 2) the expected harmonic modes have “relatively” compact supports in the Fourier domain. If classic wavelets do correspond to filters mostly localized on compact supports, the partitioning of the Fourier line follows a certain pattern (for instance the classic dyadic case uses a ratio of two to define the length of consecutive supports). Unfortunately, there is no guarantee that a given support will capture one single harmonic mode, but it could either split a mode into several subbands, or combine the information of several modes into one subband. These situations are depicted on the top part
of Figure 1.

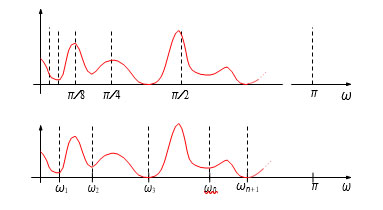
Figure 1. Top: Classic dyadic partitioning. Bottom: Adaptive partitioning. (See [1].)

Instead of using such fixed partitions, empirical wavelet filters adopt the use of adaptive partitions of the Fourier domain. Thus, the initial step consists in detecting the boundaries which separate the supports corresponding to the expected harmonic modes, see the bottom part of Figure 1. We proposed several algorithms to detect such boundaries, especially we developed a very efficient parameterless scale-space based technique [3]. Next, we build the wavelet fil- ters based on each support. In [1], the definition of these filters corresponds to Littlewood-Paley type operators, inspired by the construction in the Fourier do- main of Meyer’s wavelets. Finally, given that filter bank, the empirical wavelet transform is easily obtained by pointwise multiplication in the Fourier domain and then the inverse Fourier transform. The accurate time-frequency represen- tation is finally obtained by merging the instantaneous amplitude and frequency information of the analytical version (using the Hilbert transform) of each filter output.

In [2], we extended this idea to the 2D case for image processing purposes. Such generalization naturally arises if we again take the point of view of detect- ing adapted partitions of the Fourier domain. For instance, in [2], we revisited some classic Fourier partitions: 1) tensor, i.e., each dimension is processed sep- arately, 2) Littlewood-Paley to focus on the notion of scales, and 3) curvelets which extract specific scales and orientations. An example of such partitions is provided in Figure 2(a), (b), and (c).

These partitions provide a great level of flexibility, however, they still have some geometric shape constraints (they either correspond to rectangular boxes, rings or polar wedges). To overcome this issue, in [7], we investigate empirical wavelet filters based on arbitrary supports. The detection of such supports of arbitrary geometry is obtained by first finding the local maxima corresponding to the harmonic modes (this can be achieved by a 2D version of the scale-space method mentioned earlier), then the watershed transform is used to find the expected supports. An example of such watershed based partition is given in Figure 2(d).

Since wavelets are widely used to characterize texture, in [4] - [7], we explored the use of empirical wavelet for both unsupervised and supervised texture segmentation. We showed that empirical wavelets are very efficient in providing “optimal” features that can be used to feed some classification algorithms (k- means, spectral clustering, neural networks,…). These features help increasing the overall segmentation performances up to 15% in some texture datasets. In [7], we also proposed some preliminary investigations in texture deblurring.

Recently, in [8], we studied the theoretical properties of empirical wavelets in the 1D continuous case. We defined the appropriate formalism which provides a general framework to build empirical wavelets. This framework allows us to build empirical wavelets based on different types of mother wavelet functions (Meyer, Shannon, and Gabor, for instance). It also opens the door of using mother wavelets defined in the time domain. We provided the necessary conditions to guarantee the existence of the inverse transform.

If empirical wavelets have already been successfully used in many applica- tions in science or engineering, many aspects and questions must be addressed: can we characterize bounds of empirical frames? How to include orthogonality? How to reformulate the characterization of  Besov/Triebel-Lizorkin spaces by means of empirical wavelet coefficients? Furthermore, several aspects of the empirical wavelets let us suppose that they could provide an appropriate frame- work to model and better understand neural networks. We expect to address all of these questions within the upcoming years.

References:

[1.] J. Gilles, “Empirical Wavelet Transform,” in IEEE Trans. Signal Processing, Vol. 61, No. 16, 3999–4010, 2013, DOI: 10.1109/TSP.2013.2265222.

[2.] J. Gilles, G. Tran, and S. Osher, “2D Empirical transforms. Wavelets, Ridgelets and Curvelets Revisited,” SIAM Journal on Imaging Sciences, Vol. 7, No. 1, 157–186, 2014. 

[3.] J. Gilles and K. Heal, “A parameterless scale-space approach to find meaningful modes in histograms - Application to image and spectrum segmentation,” International Journal of Wavelets, Multiresolution and Information Processing, Vol. 12, No. 6, 1450044-1–1450044-17, 2014.

[4.] Y. Huang, V. De Bortoli, F. Zhou, and J. Gilles, “Wavelet based unsupervised texture segmentation, advantage of adaptive wavelets,” IET Image Processing, Vol. 12, No. 9, 1626–1638, 2018.

[5.] Y. Huang, F. Zhou, and J. Gilles, “Empirical curvelet based Fully Convolutional Network for supervised texture image segmentation,” Neurocomputing, Vol. 349, 31–43, 2019. 

[6.] K. Bui, A. Ciomaga, J. Gilles, J. Fauman, D. Kes, and L. Torres, “Segmentation of microscopy images based on background and texture decomposition,” Pattern Analysis and Applications, Vol. 23, 625–651, 2020.

[7.] B. Hurat, Z. Alvarado, and J. Gilles. “The Empirical Watershed Wavelet,” Journal of Imaging, Special Issue 2020 Selected Papers from Journal of Imaging Editorial Board Members,” Vol. 6, No. 12, 140, 2020. 

[8.] J. Gilles, “Continuous empirical wavelets systems,” Advances in Data Science and Adaptive Analysis, Vol. 12, No. 03n04, 2050006, 2020.