A Primer on Zeroth-Order Optimization in Signal Processing and Machine Learning: Principals, Recent Advances, and Applications

Zeroth-order (ZO) optimization is a subset of gradient-free optimization that emerges in many signal processing and machine learning (ML) applications. It is used for solving optimization problems similarly to gradient-based methods. However, it does not require the gradient, using only function evaluations. Specifically, ZO optimization iteratively performs three major steps: gradient estimation, descent direction computation, and the solution update. In this article, we provide a comprehensive review of ZO optimization, with an emphasis on showing the underlying intuition, optimization principles, and recent advances in convergence analysis. Moreover, we demonstrate promising applications of ZO optimization, such as evaluating robustness and generating explanations from black-box deep learning (DL) models and efficient online sensor management.

Zeroth-order (ZO) optimization is a subset of gradient-free optimization that emerges in many signal processing and machine learning (ML) applications. It is used for solving optimization problems similarly to gradient-based methods. However, it does not require the gradient, using only function evaluations. Specifically, ZO optimization iteratively performs three major steps: gradient estimation, descent direction computation, and the solution update. In this article, we provide a comprehensive review of ZO optimization, with an emphasis on showing the underlying intuition, optimization principles, and recent advances in convergence analysis. Moreover, we demonstrate promising applications of ZO optimization, such as evaluating robustness and generating explanations from black-box deep learning (DL) models and efficient online sensor management.

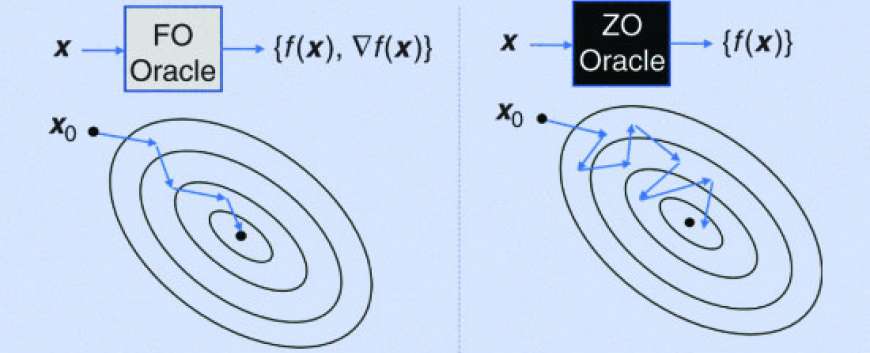
Many signal processing, ML, and DL applications involve tackling complex optimization problems that are difficult to solve analytically. Often, the objective function itself may not be in an analytical closed form, permitting function evaluations but not gradient assessments. Optimization corresponding to these types of problems falls into the category of ZO optimization with respect to black-box models, where explicit expressions of the gradients are difficult to compute or infeasible to obtain. ZO optimization methods are gradient-free counterparts of first-order (FO) optimization methods.