Sparse Representation for Wireless Communications: A Compressive Sensing Approach

Sparse representation can efficiently model signals in different applications to facilitate processing. In this article, we will discuss various applications of sparse representation in wireless communications, with a focus on the most recent compressive sensing (CS)-enabled approaches. With the help of the sparsity property, CS is able to enhance the spectrum efficiency (SE) and energy efficiency (EE) of fifth-generation (5G) and Internet of Things (IoT) networks.

This article starts from a comprehensive overview of CS principles and different sparse domains potentially used in 5G and IoT networks. Then we introduce recent research progress in applying CS to address the major opportunities and challenges in these networks, including wide-band spectrum sensing in cognitive radio networks (CRNs), data collection in IoT networks, and channel estimation and feedback in massive multiple-input, multiple-output (MIMO) systems. Moreover, we identify other potential applications and research challenges for sparse representation for 5G and IoT networks. This article will provide readers a clear picture of how to exploit sparsity properties to process wireless signals in different applications.

Introduction
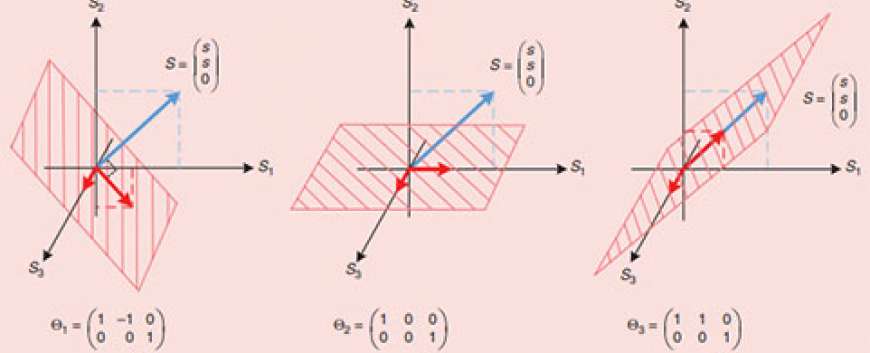
Sparse representation expresses some signals as a linear combination of a few atoms from a prespecified and overcomplete dictionary [1]. This form of sparse (or compressible) structure arises naturally in many applications [2]. For example, audio signals are sparse in the frequency domain, especially for the sounds representing tones. Image processing can exploit a sparsity property in the discrete cosine domain, i.e., many images’ discrete cosine transform (DCT) coefficients are zero or small enough to be regarded as zero. This type of sparsity property has enabled intensive research on signal and data processing, such as dimension reduction in data science, wideband sensing in CRNs, data collection in large-scale wireless sensor networks (WSNs), and channel estimation and feedback in massive MIMO.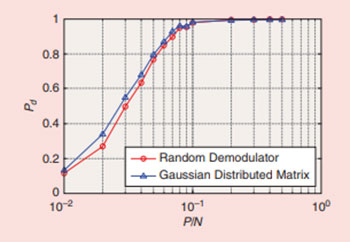 

Traditionally, signal acquisition and transmission adopt the procedure with sampling and compression. As massive connectivity is expected to be supported in the 5G and IoT networks, the amount of generated data becomes huge. Therefore, signal processing has been confronted with challenges regarding high sampling rates for data acquisition and large amounts of data for storage and transmission, especially in IoT applications with power-constrained sensor nodes. Except for developing more advanced sampling and compression techniques, it is natural to ask whether there is an approach to achieving signal sampling and compression simultaneously.

As an appealing approach to employing sparse representation, Candès proposed CS for reducing data acquisition costs by enabling sub-Nyquist sampling [3]. Based on his advanced theory [4], CS has been widely applied in many areas. The key idea in CS is to enable exact signal reconstruction from far fewer samples than required by the Nyquist– Shannon sampling theorem, provided that the signal admits a sparse representation in a certain domain. In CS, compressed samples are acquired via a small set of nonadaptive, linear, and usually randomized measurements, and signal recovery is usually formulated as an l0 -norm minimization problem to find the sparsest solution satisfying the constraints. Since l0 -norm minimization is an NP-hard problem, most of the existing CS research contributions solve it by either approximating it to a convex l1-norm minimization problem [4] or adopting greedy algorithms, such as orthogonal match pursuit (OMP).

It is often the case that the sparsifying transformation is unknown or difficult to determine. Therefore, projecting a signal to its proper sparse domain is essential in many applications that invoke CS. In 5G and IoT networks, the identified sparse domains mainly include the frequency, spatial, wavelet, and DCT domains. CS can be used to improve the SE and EE for these networks. By enabling the unlicensed use of spectrum, CRNs exploit spectral opportunities over a wide frequency range to enhance the network SE. In wide-band spectrum sensing, spectral signals naturally exploit a sparsity property in the frequency domain because of the low utilization of spectrum [5], [6], which enables sub-Nyquist sampling on cognitive devices.

Another interesting scenario is a small amount of data collection in large-scale WSNs with power-constrained sensor nodes, such as smart meters monitoring infrastructure in IoT applications. In particular, the monitoring readings usually have a sparse representation in the DCT domain because of the temporal and spatial correlations [7]. CS can be applied to enhance the EE of WSNs and to extend the lifetime of sensor nodes.