Optimize Your Signal Processing with Bayesian Optimization
Top Reasons to Join SPS Today!
1. IEEE Signal Processing Magazine
2. Signal Processing Digital Library*
3. Inside Signal Processing Newsletter
4. SPS Resource Center
5. Career advancement & recognition
6. Discounts on conferences and publications
7. Professional networking
8. Communities for students, young professionals, and women
9. Volunteer opportunities
10. Coming soon! PDH/CEU credits
Click here to learn more.
Optimize Your Signal Processing with Bayesian Optimization
Signal processing is a fundamental discipline that underpins countless technological advancements, from audio and image enhancement [1] to wireless communications and sensor networks [2]. As the field continues to evolve, researchers and engineers are always on the lookout for techniques that can help them optimize complex, noisy, and expensive-to-evaluate objective functions often encountered in signal processing problems. Bayesian optimization (BO) is a powerful optimization framework that is gaining traction in the signal processing community [3]. In this blog post, we will explore the intuition behind BO, discuss its key advantages over traditional optimization methods, and showcase some real-world applications where it has delivered promising results.
What is Bayesian Optimization?
Unlike traditional optimization methods that rely on gradient information or exhaustive search, BO takes a more principled approach by using a probabilistic model to guide the optimization process. The key intuition behind BO is the use of a surrogate model, typically a Gaussian process, to capture the underlying structure of the objective function being optimized. This surrogate model allows the algorithm to make informed predictions about the objective function’s behaviour.
The strength of BO lies in its ability to balance exploration and exploitation. At each step, the algorithm determines the next point to evaluate based on a carefully designed acquisition function, which takes into account both the predicted value of the objective function (exploitation) and the uncertainty in the model’s predictions (exploration). This balance allows BO to efficiently locate the global optimum, even in complex and noisy scenarios.
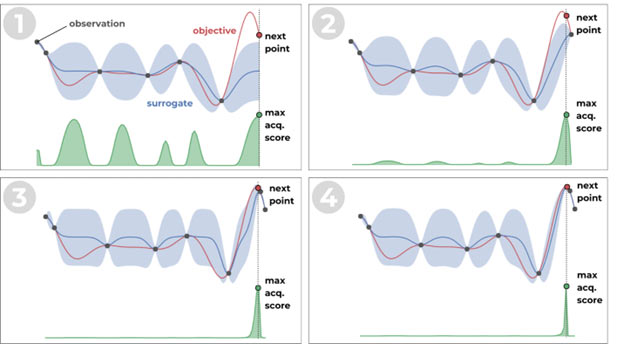
Figure 1: Illustration of the Bayesian optimization process. Created by Author.
An illustration of the BO process is given in Figure 1. The figure shows how the surrogate model (a Gaussian process) is used to guide the optimization process, with the acquisition function determining the next point to evaluate. As the algorithm progresses, the surrogate model is updated, and the optimization converges towards the global optimum of the objective function.
Why Bayesian Optimization?
BO offers several key advantages for signal processing applications compared to traditional methods, including:
- Black Box Optimization
BO excels at optimizing “black box” objective functions, where the underlying relationships between the input and the output are unknown or difficult to model analytically. This makes BO a powerful tool for signal processing applications where the system behaviour can be complex or not fully understood. - Sample Efficiency
BO is known for its sample efficiency, meaning it can often find the optimal solution with far fewer objective function evaluations than other techniques, such as grid search or random search. This is particularly valuable when dealing with computationally intensive signal processing tasks, as it reduces the overall time and resources required to find the optimal configuration. - Robustness
BO is robust to noisy objective functions, making it well-suited for real-world signal processing problems where measurements may be imperfect or subject to environmental interference. By modelling the uncertainty in the objective function, BO can still make informed decisions and converge to the optimal solution, even in the presence of noise or other sources of uncertainty.
Success Stories of Bayesian Optimization
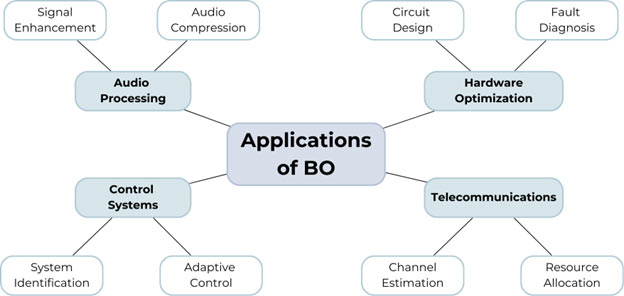
Figure 2: Applications of Bayesian optimization in signal processing. Created by Author.
BO has already found success in various signal processing applications, such as:
- High-Speed Channel Optimization
Researchers have employed BO to enhance the design of high-speed channels by optimizing their frequency response characteristics, particularly focusing on minimizing insertion loss [4]. This optimization process involves identifying the optimal physical dimensions of channel components, such as traces, vias, and connectors, which are critical for maintaining signal integrity in high-speed data transmission. - Analog Circuit Design
BO has been used to automate analog circuit sizing [5]. By using Gaussian processes to model the circuit’s performance, the proposed method can efficiently navigate the high-dimensional design space and identify optimal configurations with significantly fewer computationally-intensive circuit simulations compared to traditional methods. - Nonlinear System Identification
The authors of the work presented in [6] introduced a digital signal processing (DSP) scheme that leverages BO to enhance the performance of cognitive optical transmitters. The proposed scheme performs hyperparameter tuning to autonomously optimize the memory tap distribution of Volterra series and adapt the parameters used in the synthetization of a digital pre-distortion (DPD) filter.
The Future of Bayesian Optimization
With its ability to handle complex, noisy, and computationally expensive objective functions, BO has become an increasingly valuable tool for signal processing engineers. As the algorithmic advancements and computational power continue to improve, we can expect to see BO being applied to an even wider range of signal processing problems, from hardware optimization to advanced signal processing algorithms.
References:
[1] W. Zhang, P. Zhuang, H. -H. Sun, G. Li, S. Kwong and C. Li, “Underwater Image Enhancement via a Fast yet Effective Traditional Method,” IEEE SPS Blog, 2023.
[2] A. M. Elbir, K. V. Mishra, S. A. Vorobyov and R. W. Heath, “An Echo in Time: Tracing the Evolution of Beamforming Algorithms,” IEEE SPS Blog, 2023.
[3] B. Shahriari, K. Swersky, Z. Wang, R. P. Adams and N. de Freitas, “Taking the Human Out of the Loop: A Review of Bayesian Optimization,” in Proceedings of the IEEE, vol. 104, no. 1, pp. 148-175, Jan. 2016, doi: https://dx.doi.org/10.1109/JPROC.2015.2494218.
[4] D. Lho et al., “Bayesian Optimization of High-Speed Channel for Signal Integrity Analysis,” 2019 IEEE 28th Conference on Electrical Performance of Electronic Packaging and Systems (EPEPS), Montreal, QC, Canada, 2019, pp. 1-3, doi: https://dx.doi.org/10.1109/EPEPS47316.2019.193211.
[5] W. Lyu et al., “An Efficient Bayesian Optimization Approach for Automated Optimization of Analog Circuits,” in IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 65, no. 6, pp. 1954-1967, June 2018, doi: https://dx.doi.org/10.1109/TCSI.2017.2768826.
[6] M. Sena et al., “Bayesian Optimization for Nonlinear System Identification and Pre-Distortion in Cognitive Transmitters,” in Journal of Lightwave Technology, vol. 39, no. 15, pp. 5008-5020, Aug.1, 2021, doi: https://dx.doi.org/10.1109/JLT.2021.3083676.
SPS Social Media
- IEEE SPS Facebook Page https://www.facebook.com/ieeeSPS
- IEEE SPS X Page https://x.com/IEEEsps
- IEEE SPS Instagram Page https://www.instagram.com/ieeesps/?hl=en
- IEEE SPS LinkedIn Page https://www.linkedin.com/company/ieeesps/
- IEEE SPS YouTube Channel https://www.youtube.com/ieeeSPS








