
Contributed by Prof. Zicheng Liu, based on the IEEEXplore® article, “Physics-Guided Loss Functions Improve Deep Learning Performance in Inverse Scattering” published in the IEEE Transactions on Computational Imaging in March 2022, and the SPS Webinar, Guiding Artificial Intelligence Through Physics for Scientific Problems, available on the SPS Resource Center.
Guide
Due to the ability of noninvasive imaging of internal structures, electromagnetic inverse scattering problems (ISPs) [1] are widely studied in industrial applications including remote sensing, biomedical imaging, non-destructive testing and geophysics. Images are obtained by collecting the fields scattered by the objects and reconstructing the distribution of electromagnetic constitutive parameters (relative permittivity and conductivity) of the objects. Deep neural network (DNN) techniques have been successfully applied on ISPs and shown potential of superior imaging over conventional methods [2]. However, the imaging performance is hard to explain due to the black-box nature of DNN solvers.
In this blog, we introduced physics-inspired loss functions which guide the network to have prediction performances which can explainable.
Inverse Scattering Problems
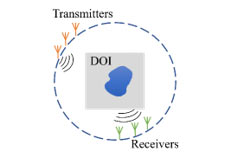
Figure 1: Imaging scenario with multiple transmitters and receivers.
The concerned imaging scenario is sketched in Fig. 1. Electromagnetic waves are transmitted by a transmitter and the wave propagation is disturbed due to existence of scatterers in domain of interest (DOI). Recording the disturbance (scattered fields) with the deployed receivers around DOI, the information about the scatterers has the chance to be reconstructed. Such information is a distribution of contrast which is shown as the image of the scatterers. Multiple transmitters can be used to achieve better imaging performance as a result of “observations” from various angles.
Deep Neural Network Solvers
Deep neural network (DNN) solvers are data-driven methods. It is nature to take scattered fields and the predicted scatterer image as the input and response of DNN solvers, respectively. However, the data mapping relation from the fields to the scatterer image is complex and learning this relation can be challenging in terms of generalization ability, reconstruction accuracy and stability. Incorporating physics-guided priors are helpful to enhance the learning ability.
Physics
The disturbance on the field propagation by scatterers can be explained by Maxwell equations. The polarization of incident wave leads to induced currents which generate scattered fields and change the field distribution inside and outside scatterers. In mathematics, the inducted current and the field inside the scatterers is as a function of contrast distribution of scatterers [1]. Such prior knowledge is made use of with the physics-guided loss functions in DNN solvers.
Physics-guided Loss Functions
Two physics-guided loss functions are explored. respectively. In addition to the mean squared error (MSE) of the discrepancy between the predicted contrast and the ground truth [3], the first one, denoted by L1, makes use of the knowledge of induced current. Since the distribution of induced current and that of contrast share the common geometric characters, feature-enhanced imaging is expected. The other, denoted by L2, taking the fields inside the scatterers as the additional constraint to contrast, since the fields inside scatterers are sensitive to the existence of artifacts and debris, the noise robustness is expected to be enhanced.
Imaging Example
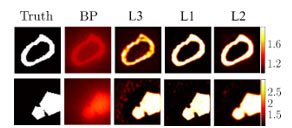
Figure 2: Example of imaging results with physics-guided loss functions. L3 only penalizing contrast discrepancy, L1 and L2 additionally make use of induced current and fields inside scatterers, respectively.
Inputting the initial estimate of contrast distribution into the U-net neural network [3], three DNN solvers are obtained with loss function L1, L2, and L3, respectively. L3 only penalizes contrast discrepancy. The imaging results are shown in Fig. 2.
More information of this paper can be obtained from the article.
References:
[1] X. Chen, Computational Methods for Electromagnetic Inverse Scattering, Hoboken, NJ, USA: Wiley, 2018, doi: https://dx.doi.org/10.1002/9781119311997.
[2] X. Chen, Z. Wei, M. Li and P. Rocca, "A review of deep learning approaches for inverse scattering problems", Progress in Electromagnetics Research, vol. 167, pp. 67-81, doi: https://dx.doi.org/ 10.2528/pier20030705.
[3] Z. Wei and X. Chen, "Deep-learning schemes for full-wave nonlinear inverse scattering problems", in IEEE Transactions on Geoscience and Remote Sensing, vol. 57, no. 4, pp. 1849-1860, doi: https://dx.doi.org/10.1109/TGRS.2018.2869221.
