Robust Subspace Learning

Principal component analysis (PCA) is one of the most widely used dimension reduction techniques. A related easier problem is termed subspace learning or subspace estimation. Given relatively clean data, both are easily solved via singular value decomposition (SVD). The problem of subspace learning or PCA in the presence of outliers is called robust subspace learning (RSL) or robust PCA (RPCA). For long data sequences, if one tries to use a single lower-dimensional subspace to represent the data, the required subspace dimension may end up being quite large. For such data, a better model is to assume that it lies in a low-dimensional subspace that can change over time, albeit gradually. The problem of tracking such data (and the subspaces) while being robust to outliers is called robust subspace tracking (RST). This article provides a magazine-style overview of the entire field of RSL and tracking. In particular, solutions for three problems are discussed in detail:

RSR assumes that an entire data vector is either an outlier or an inlier. The S+LR formulation instead assumes that outliers occur on only a few data vector indices and, hence, are well modeled as sparse corruptions.

 

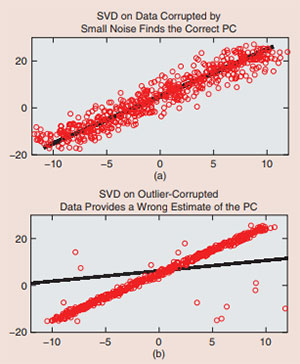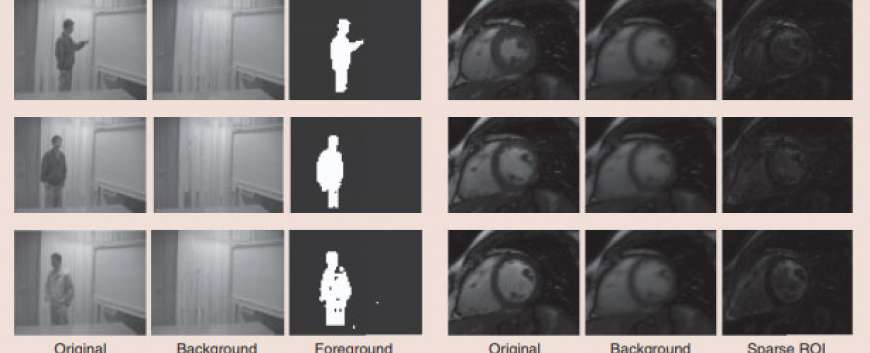
PCA finds application in a variety of scientific and data analytics’ problems ranging from exploratory data analysis and classification, e.g., image retrieval or face recognition, to a variety of modern applications such as video analytics, recommendation system design, and understanding social networks dynamics. PCA finds a small number of orthogonal basis vectors, called principal components (PCs), along which most of the variability of the data set lies. In most applications, only the subspace spanned by the PCs (principal subspace) is of interest. For example, this is all that is needed for dimension reduction. This easier problem is typically called subspace learning or subspace estimation: the two terms are sometimes used interchangeably. Given a matrix of clean data, PCA is easily accomplished via SVD on the data matrix. The same problem becomes much harder if the data is corrupted by even a few outliers. The reason is that SVD is sensitive to outliers. We show an example of this in Figure 1. In today’s big data age, since data is often acquired using a large number of inexpensive sensors, outliers are becoming even more common. They occur due to various reasons such as node or sensor failures, foreground occlusion of video sequences, or abnormalities or other anomalous behavior on certain nodes of a network. The harder problem of PCA or subspace learning for outlier corrupted data is called RPCA or RSL.

 

Since the term outlier does not have a precise mathematical meaning, the RPCA problem was, until recently, not well defined. Even so, many classical heuristics existed for solving it, e.g., see [1] and [2] and references therein. In recent years, there have been multiple attempts to qualify this term. Most popular among these is the idea of treating an outlier as an additive sparse corruption, which was popularized in the work of Wright and Ma [3]. This is a valid definition because it models the fact that outliers occur infrequently and allows them to have any magnitude. In particular, their magnitude can be much larger than that of the true data points. Using this definition, the recent work by Candès et al. [4] defined RPCA as the problem of decomposing a given data matrix, M, into the sum of a low-rank matrix, L, whose column subspace gives the PCs and a sparse matrix (outliers’ matrix), S. This definition, which is often referred to as the S+LR formulation, has led to numerous interesting new works on RPCA solutions, many of which are provably correct under simple assumptions, e.g., [4]–[10]. A key motivating application is video analytics: decomposing a video into a slowly changing background video and a sparse foreground video [2], [4]; see an example in Figure 2(a). The background changes slowly, and the changes are usually dense (not sparse). It is thus well modeled as a dense vector that lies in the low-dimensional subspace of the original space [4]. The foreground usually consists of one or more moving objects, and is thus correctly modeled as the sparse outlier.