Closed-Form Impulse Responses of Linear Time-Invariant Systems: A Unifying Approach
Top Reasons to Join SPS Today!
1. IEEE Signal Processing Magazine
2. Signal Processing Digital Library*
3. Inside Signal Processing Newsletter
4. SPS Resource Center
5. Career advancement & recognition
6. Discounts on conferences and publications
7. Professional networking
8. Communities for students, young professionals, and women
9. Volunteer opportunities
10. Coming soon! PDH/CEU credits
Click here to learn more.
Closed-Form Impulse Responses of Linear Time-Invariant Systems: A Unifying Approach
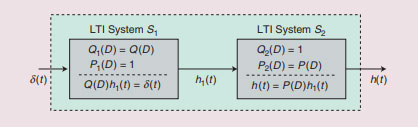
In many signal processing applications, filtering is accomplished through linear time-invariant (LTI) systems described by linear constant-coefficient differential and difference equations since they are conveniently implemented using either analog or digital hardware [1]. An LTI system can be completely characterized in the time domain by its impulse response or in the frequency domain by its frequency response, which is the Fourier transform of the system’s impulse response. Equivalently, using the Laplace transform [or the z-transform in the case of discrete-time (DT) systems] as a generalization of the Fourier transform, any continuous-time (CT) or DT LTI system can be characterized by its transfer function (or system function) in the s-domain or the z-domain, respectively. In this article, we explain how to find impulse responses of LTI systems described by differential and difference equations directly in the time domain without resorting to any transform methods or recursive procedures.
Relavance - In the literature, the topic of finding impulse responses of LTI systems directly in the time domain has not received proper attention for the following reasons. First, there are approaches based on transform methods. Second, in the case of DT systems, even the impulse response of an LTI system can be obtained recursively.
For these reasons, in the signal processing community, there are various groups of researchers that have different opinions regarding this topic. There is one group that has no interest in finding the impulse response of an LTI system directly in the time domain since it can be obtained based on transform methods [7]–[10]. This kind of approach implies that the topic of time-domain analysis of LTI systems is handicapped and incomplete since it is mostly relied on the frequency-domain analysis. However, the following logical question arises: “Why do we need to resort to a transformation to find the impulse response of a system that is one of the characteristics of the system in the time domain?”
There is another group of researchers that thinks it may not be possible to determine a closed-form solution for the impulse response of a DT LTI system described by a difference equation [5], [6]. However, there are some researchers who have been trying to obtain closedform expressions for impulse responses of LTI systems without resorting to transform methods or recursive procedures. In the literature [1]–[4], it has been shown how a closed-form expression for the impulse response of a CT LTI system described by a differential equation can be obtained in the time domain. Even in [1]–[4], the same problem has been tackled for DT LTI systems described by difference equations but with a completely different method from the one for CT systems. Because of two different methods and not treating CT and DT systems in parallel, none of those approaches can be considered as a unifying approach. In other words, the disadvantage of all those approaches is because of a lack of sharing insight and intuition between CT and DT systems in the time domain.
Prerequisites - To understand this article, the prerequisites consist of basic calculus and the fundamentals of signal and system analysis. Some familiarity with homogeneous differential and difference equations is necessary. Also, in particular, a background in the topic of time-domain analysis of LTI systems is required.
SPS Social Media
- IEEE SPS Facebook Page https://www.facebook.com/ieeeSPS
- IEEE SPS X Page https://x.com/IEEEsps
- IEEE SPS Instagram Page https://www.instagram.com/ieeesps/?hl=en
- IEEE SPS LinkedIn Page https://www.linkedin.com/company/ieeesps/
- IEEE SPS YouTube Channel https://www.youtube.com/ieeeSPS














