What Should We Learn? Special Issue on Robust Subspace Learning and Tracking

Subspace learning theory for dimensionality reduction was initiated with the Principal Component Analysis (PCA) formulation proposed by Pearson in 1901. PCA was first widely used for data analysis in the field of psychometrics and chemometrics but today it is often the first step in more various types of exploratory data analysis, predictive modeling, classification and clustering problems. It finds modern applications in signal processing, biomedical imaging, computer vision, process fault detection, recommendation system design and many more domains. Since one century, numerous other subspace learning models, either reconstructive and discriminative, were developed over time in literature to address dimensionality reduction while keeping the relevant information in a different manner from PCA. However, PCA can also be viewed as a soft clustering method that seeks to find clusters in different subspaces within a dataset, and numerous clustering methods are based on dimensionality reduction. These methods are called subspace clustering methods that are extension of traditional PCA based clustering, and divide data points belonging to the union of subspaces (UoS) into the respective subspaces. In several modern applications, the main limitation of the subspace learning and clustering models are their sensitivity to outliers. Thus, further developments concern robust subspace learning which refers to the problem of subspace learning in the presence of outliers. In fact, even the classical subspace learning problem with speed or memory constraints is not a solved problem. These issues have become practically important for modern datasets because of the following reasons:

• The data and noise maybe correlated in several applications, i.e. need for correlated subspace learning.
• The data matrix is often so large that it cannot be directly stored in the computers memory, i.e. need for streaming subspace learning solutions.
• The data are held at different locations, i.e. need for distributed PCA algorithms to harness local communications and network connectivity to avoid communicating and accessing the entire array locally.
• The data are observed in high-dimension but PCA is usually linear combinations of all input variables. Thus, it encounters great fundamental challenges under high dimensionality and may produce wrong results under high-dimensionality, i.e. need for sparse PCA and scalable PCA algorithms.
• A lot of today data consist of missing entries and/or outlier corrupted entries: i.e. need for matrix completion, robust PCA and robust subspace recovery.
• A lot of data today arrive sequentially, the data subspace itself may change over time, the entire dataset cannot be stored but short buggers can be and decisions are often needed in real-time or near real-time, i.e. need for subspace tracking and dynamic RPCA.
• Many types of data are better represented as a tensor dataset rather than a vector dataset or matrix, i.e. need for tensor PCA/RPCA.

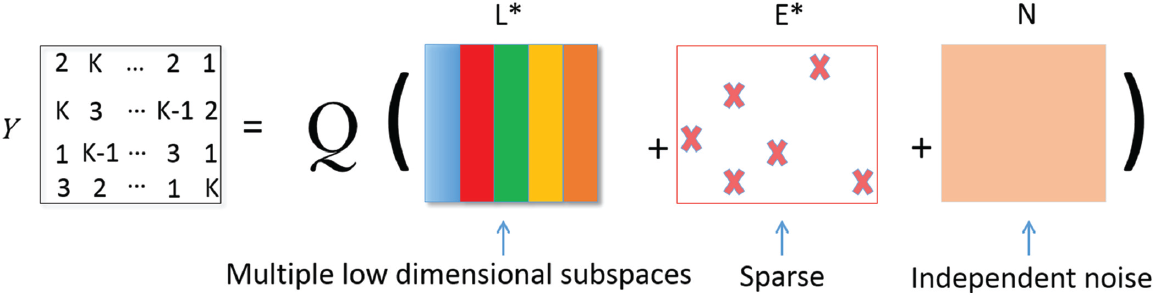
Thus, the special issue on Robust Subspace Learning and Tracking published in IEEE Journal of Selected Topics in Signal Processing in December 2018 group recent works in robust subspace learning and clustering related to theory, algorithms and applications for signal processing and computer vision applications. Several papers concern algorithms to address robustness of subspace learning against different kinds of outliers.